- Magnetic particle imaging and reconstruction on Lissajous curves
- Mathematical analysis of models in magnetic particle imaging.
- Polynomial interpolation schemes on Lissajous-Chebyshev points
- Iterative solvers for linear inverse problems
- Space-frequency analysis and polynomial spaces
- Uncertainty principles on Riemannian manifolds
Magnetic Particle Imaging (MPI) and reconstruction on Lissajous curves
Magnetic Particle Imaging (MPI) is a novel biomedical imaging modality in which the
spatial distribution of superparamagnetic nanoparticles is determined by the non-linear magnetization response of the
particles to an applied magnetic field. These applied magnetic fields are usually generated in such a way that the signal acquisition is carried
out along a closed Lissajous curve.
This raises the natural question how a continuous function or discretized data values
along Lissajous trajectories can be extended into the surrounding region. Further, in MPI usually only a finite number of
Fourier coefficients of the signal on the acquisition trajectory are measured. This leads directly to the fascinating
mathematical question how a multivariate density function can be approximately recovered from limited spectral data on a curve.
In 2014, I initiated with several colleagues from different universities and industry the DFG-funded interdisciplanary scientific network
"Development, analysis and application of mathematical methods for Magnetic Particle Imaging (MathMPI) "
in which mathematical questions related to the imaging modality MPI are tackled.

Fig. 1: Reconstruction of magnetic particle distributions based on Chebyshev spectral methods for data measured along Lissajous curves. Left: Particle density reconstructed on Lissajous node points. Middle left: Chebyshev reconstruction without filtering. Middle right: Chebyshev reconstruction with classical spectral filtering. Right: Chebyshev reconstruction with adaptive spectral filtering.
In the framework of this network we systematically studied mathematical questions related to the structure of Lissajous curves, its discretizations
and the interpolation and approximation of data along these trajectories. Similar as in the theory of the Padua points, we developed a
Chebyshev spectral method for an efficient polynomial interpolation on the node points of two- and higher dimensional Lissajous curves and applied them for
the reconstruction in MPI. In particular, we studied Lissajous node points as a possibility to reduce MPI measurements and to obtain efficient and fast
reconstructions at the same time. A second focus of research is the development of spectral basis elements such that the MPI system matrix can
be represented and stored in a sparse way. A third goal is the construction of adaptive spectral filters in order to improve the reconstruction quality
of the Chebyshev spectral methods.
This research was done in collaboration with the Institute of Medical Engineering at the University of Lübeck and the Institute of Biomedical Imaging at the UKE in Hamburg.
The adaptive spectral filters were developed in collaboration with the Padova-Verona research group on Constructive Approximation and Applications.
Publications
- Erb, W., Kaethner, C., Ahlborg, M. and Buzug, T.M. Bivariate Lagrange interpolation at the node points of non-degenerate Lissajous curves Numer. Math. 133, 4 (2016), 685-705 (Preprint)
- Erb, W., Kaethner, C., Dencker, P. and Ahlborg, M. A survey on bivariate Lagrange interpolation on Lissajous nodes Dolomites Research Notes on Approximation 8 (Special issue) (2015), 23-36 (Publication)
- Kaethner, C., Erb, W., Ahlborg, M., Szwargulski, P., Knopp, T. and Buzug, T. M. Non-Equispaced System Matrix Acquisition for Magnetic Particle Imaging based on Lissajous Node Points IEEE Transactions on Medical Imaging 35, 11 (2016), 2476-2485
- Schmiester, L., Moddel, M., Erb, W. and Knopp, T. Direct Image Reconstruction of Lissajous Type Magnetic Particle Imaging Data using Chebyshev-based Matrix Compression IEEE Transactions on Computational Imaging 3, 4 (2017), 671-681
- De Marchi, S., Erb, W. and Marchetti, F. Spectral filtering for the reduction of the Gibbs phenomenon for polynomial approximation methods on Lissajous curves with applications in MPI Dolomites Res. Notes Approx. 10 (2017), 128-137 (Publication)
Mathematical analysis of models in magnetic particle imaging
The modeling and the analysis of the imaging process in magnetic particle imaging is an ongoing research project within the research network MathMPI. In this project, we systematically investigate the continuous MPI imaging operator in different mathematical setups. We introduced suitable function spaces in which the MPI operator is decomposed into simple building blocks and in which these building blocks are analyzed with respect to their mathematical properties. In this way, we could obtain a complete analysis of the continuous 1D-MPI forward operator and, in particular, a mathematical description of it's ill-posedness. Further, we could show an exponential decay of the singular values of the 1D-MPI operator.

Formula 1: The full 1D-MPI forward operator giving the Fourier coefficients of the MPI signal.
More information on this topic can be found in the following slides.
Publications
- Erb, W., Weinmann, A., Ahlborg, M., Brandt, C., Bringout, G. , Buzug, T.M, Frikel J., Kaethner, C., Knopp, T., März, T., Möddel, M., Storath, M. and Weber, A. Mathematical Analysis of the 1D Model and Reconstruction Schemes for Magnetic Particle Imaging Inverse Problems 34 (2018) 055012 (21pp) (Preprint)
Polynomial interpolation schemes on Lissajous curves


Fig. 2: Two Lissajous figures with the respective Lissajous-Chebyshev interpolation node points.
Starting from the applications in Magnetic Particle Imaging, I developed together with P. Dencker a comprehensive theory on multivariate polynomial interpolation related to Lissajous-Chebyshev points. This theory syntesizes and generalizes interpolation results for several well-known interpolation node sets as the Padua points, the Morrow-Patterson-Xu points or node points generated by a single Lissajous curve. We could show that these points give rise to a multivariate Chebyshev spectral interpolation scheme with some remarkable properties that can be implemented as efficiently as a tensor-product Chebyshev interpolant. Further, also the numerical condition and the convergence rates of the developed scheme are equivalent to the rates of a corresponding tensor-product Chebyshev scheme.
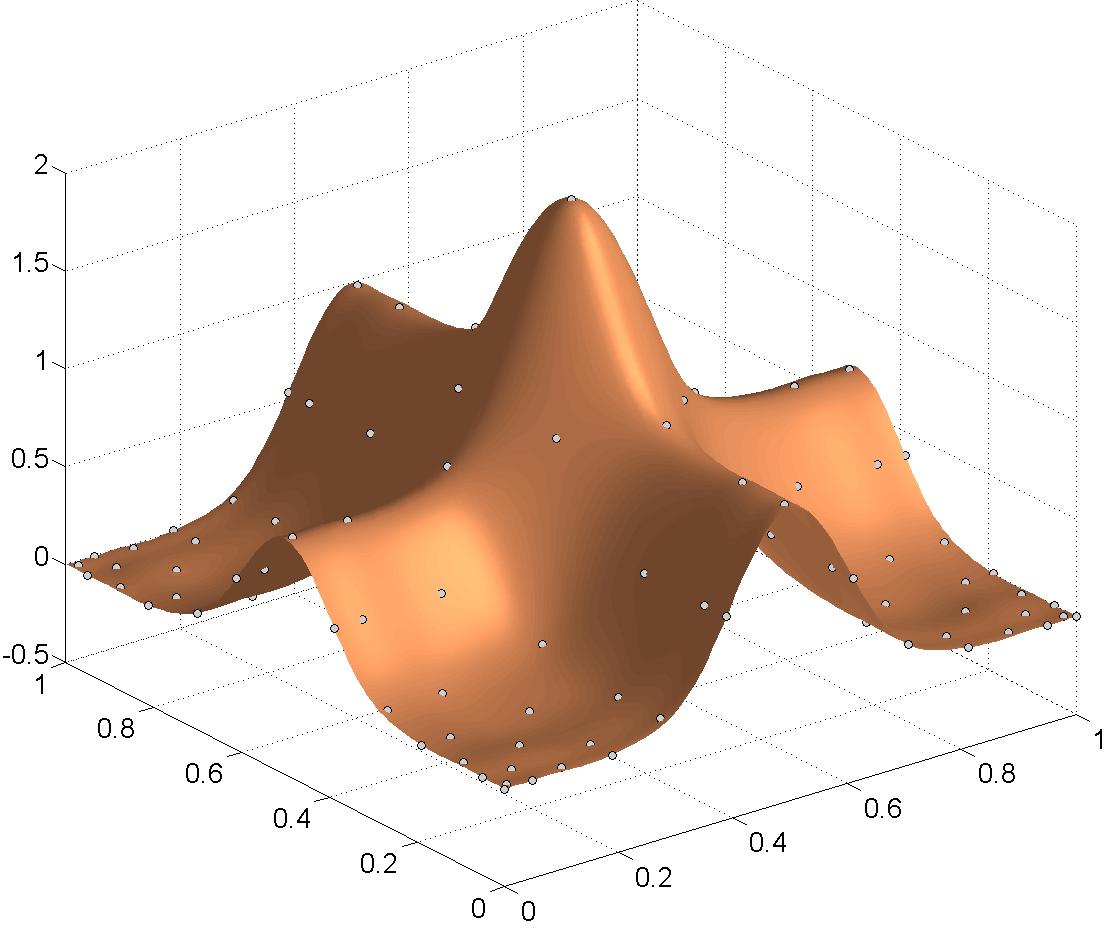

Fig. 3: Two polynomial interpolants of function values on Lissajous-Chebyshev points.
Publications
- Erb, W., Kaethner, C., Ahlborg, M. and Buzug, T.M. Bivariate Lagrange interpolation at the node points of non-degenerate Lissajous curves Numer. Math. 133, 4 (2016), 685-705 (Preprint)
- Erb, W. Bivariate Lagrange interpolation at the node points of Lissajous curves - the degenerate case Appl. Math. Comput. 289 (2016) 409-425 (Preprint)
- Erb, W., Kaethner, C. Dencker, P. and Ahlborg, M. A survey on bivariate Lagrange interpolation on Lissajous nodes Dolomites Research Notes on Approximation 8 (Special issue) (2015), 23-36 (Publication)
- Dencker, P. and Erb, W. Multivariate polynomial interpolation on Lissajous-Chebyshev nodes J. Approx. Theory, J. Approx. Theory 219 (2017), 15-45 (Preprint)
- Dencker, P., Erb, W., Kolomoitsev, Y. and Lomako, T. Lebesgue constants for polyhedral sets and polynomial interpolation on Lissajous-Chebyshev nodes Journal of Complexity 43, (2017), 1-27 (Preprint)
- Dencker, P. and Erb, W. A unifying theory for multivariate polynomial interpolation on general Lissajous-Chebyshev nodes arXiv:1711.00557 (2017) (Preprint)
Software

Fig. 4: The app LC2Dfevalapp to test polynomial interpolation schemes on general Lissajous-Chebyshev nodes.
For polynomial interpolation on general Lissajous-Chebyshev points
- LC2Ditp: A software package that contains a Matlab implementation for 2D polynomial interpolation on general Lissajous-Chebyshev points. It contains also two apps to test the interpolation schemes and to display the Lissajous-Chebyshev node points.
- LC3Ditp: A software package that contains a Matlab implementation for 3D polynomial interpolation on general Lissajous-Chebyshev points.
- LS2Ditp: This software package contains a Matlab implementation for bivariate polynomial interpolation on the node points of degenerate and non-degenerate 2D-Lissajous curves.
- LD3Ditp: A small software package that contains a Matlab implementation for 3D polynomial interpolation on the node points of degenerate 3D-Lissajous curves.
Iterative solvers for linear inverse problems
Linked to an interdisciplinary project in magnetic resonance elastography (MRE), I studied mathematical problems related to inverse problems in medical imaging. We introduced and investigated accelerated Landweber methods for linear ill-posed problems obtained by an alteration of the coefficients in the three-term recurrence relation of the semi-iterative methods. The residual polynomials of the methods under consideration are linked to a family of co-dilated ultraspherical polynomials. This connection makes it possible to control the decay of the residual polynomials at the origin by means of a dilation parameter. Depending on the data, the approximation error of the semi-iterative methods can be improved by altering this dilation parameter. The asymptotic convergence order of the new semi-iterative methods turns out to be the same as for the original methods. We tested these new algorithms and developed a simple adaptive scheme in which the dilation parameter is optimized in every iteration step. In collaboration with Dr. Semenova these semi-iterative solvers were combined with adaptive discretization methods. We showed that such an adaptive discretization approach in combination with a stopping criterion as the discrepancy principle or the balancing principle yields an order optimal regularization scheme and allows to reduce the computational costs.
Publications
- Erb, W. Accelerated Landweber methods based on co-dilated orthogonal polynomials Numer. Alg. 68, 2 (2015) 229-260
- Erb, W. and Semenova, E.V. On adaptive discretization schemes for the solution of ill-posed problems with semiiterative methods Appl. Anal. 94, 10 (2015) 2057-2076
Space-frequency analysis and polynomial spaces
Based on the uncertainty principles constructed in my Ph.D. thesis, we developed a time-frequency theory for orthogonal
polynomials that runs parallel to the time-frequency
analysis of bandlimited functions developed by Landau, Pollak and Slepian. For this purpose, the spectral decomposition of a particular compact time-frequency-
operator is studied. This decomposition and its eigenvalues are
closely related to the theory of orthogonal polynomials. Results from both
theories, the theory of orthogonal polynomials and the Landau-Pollak-Slepian
theory, can be used to prove localization and approximation properties of the
corresponding eigenfunctions. Furthermore, an uncertainty principle was proven that
reflects the limitation of coupled time and frequency locatability.
In a second work, this theory was extended successfully to spherical polynomials on the sphere.
Using weak limits related to the structure of spherical harmonics provided us with information on the
proportion of basis functions needed to approximate localized functions. One big advantage of the developed theory
is the fact that the localized basis functions can be represented and computed efficiently with orthogonal polynomials.



Fig. 5: Decomposition of a function on the unit sphere with localized polynomial basis functions.
Publications
- Erb, W. An orthogonal polynomial analogue of the Landau-Pollak-Slepian time-frequency analysis J. Approx. Theory 166 (2013) 56-77
- Erb, W. and Mathias, S. An alternative to Slepian functions on the unit sphere - A space-frequency analysis based on localized spherical polynomials Appl. Comput. Harmon. Anal. 38, 2 (2015) 222-241
Uncertainty principles on manifolds
As a PhD student, I was mainly interested in uncertainty principles on Riemannian manifolds. I was able to show that the product of a space and a frequency variance for functions on a Riemannian manifold is always larger than a particular constant. The key ingredient for the proof of this uncertainty principle is a commutator relation for particular Dunkl operators. In particular, these uncertainties turn out to be sharp. For 2-point homogeneous spaces, the space variance of the uncertainty product can be used to construct optimally space localized polynomials on symmetric spaces as the unit sphere.



Fig. 6: Illustrations of optimally space localized polynomials on the unit sphere in different spaces of spherical harmonics.
Publications
- Erb, W. Uncertainty principles on compact Riemannian manifolds Appl. Comput. Harmon. Anal. 29, 2 (2010) 182-197
- Erb, W. Uncertainty principles on Riemannian manifolds Logos Verlag Berlin (2010) Dissertation TU München
- Erb, W. Optimally space localized polynomials with applications in signal processing J. Fourier Anal. Appl. 18, 1 (2012) 45-66
Further links
- CAA: Padova-Verona research group on "Constructive Approximation and Applications"
for further information and references on Padua points and polynomial approximation on Lissajous curves - The Institute of Biomedical Imaging at the UKE in Hamburg
- Mathematical methods for Magnetic Particle Imaging (MathMPI)
for further information on the DFG-funded interdisciplanary scientific network MathMPI