A talk I gave at the ASL Annual Meeting in Ames, Iowa, May 15, 2024.
Slides:
ASL-2024-slides-Kjos-Hanssen
Category Archives: research
Automatic complexity of distinguishing
My book “Automatic complexity: a computable measure of irregularity” was published by de Gruyter on February 19, 2024. It concerns a version of Sipser’s complexity of distinguishing that was introduced by Shallit and Wang in 2001 and has been developed by me and others since 2013.
Erratum
Theorem 6.6: Two constructions $M_1\times_1 M_2$ and $M_1\times_2 M_2$ are described. The text suggests that $\times_1$ is used for the theorem, but actually $\times_2$ should be used. The operation $\times_1$ can be used to prove the inequality $A_N(x)\le A_N(x\mid y)\cdot A_N(y)$ instead.
Math 100 student’s protein folding research
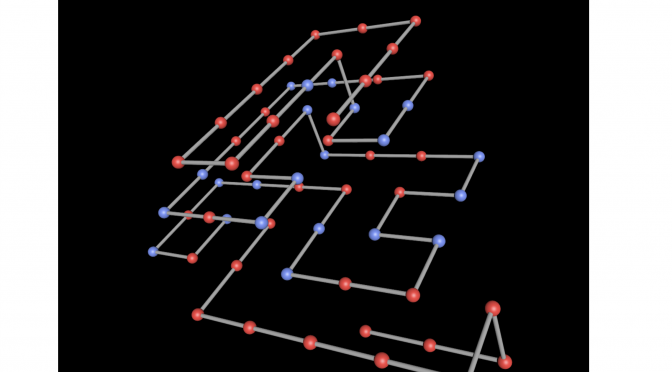
Madison Koskey had the highest score in the class on this project task:
Fold an idealized protein known as S64 to obtain a highest possible score in the hydrophobic-polar protein folding model in three dimensions.
This problem was studied by Lesh, Mitzenmacher, and Whitesides (2003).
Above we see Madison’s intricate folding of S64 which earned a score of 27.
To try your hand at rotating it in 3D, go directly to this link.
Recent PhDs
Three new papers
with my recent PhDs Birns (2023, left) and Webb (2022, right). Webb is now an Assistant Professor at Chaminade University, and Birns is a data scientist at Pacific Life in California.- KL-randomness and effective dimension under strong reducibility (with David J. Webb). Computability in Europe, Lectures Notes in Computer Science, 2021.
- On the degrees of constructively immune sets (with Samuel D. Birns). Computability in Europe, Lectures Notes in Computer Science, 2021.
- Strong Medvedev reducibilities and the KL-randomness problem (with David J. Webb). Computability in Europe, Lectures Notes in Computer Science, 2022.
The number of languages with maximum state complexity
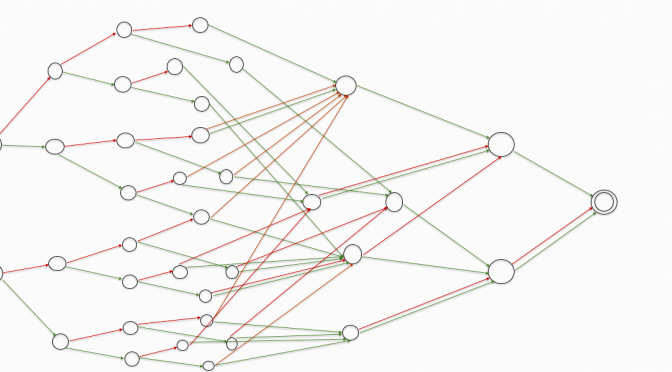
Lei Liu completed her Master’s degree with the project title Complexity of Options in 2017.
An extension to monotone options (pictured) was presented at
ALH-2018. The new paper is called The number of languages with maximum state complexity and has been accepted for TAMC 2019.
As of 2022, the paper has been through 7 revisions and has been accepted for publication in the journal Algebra Universalis.
Some of the 168 monotone Boolean functions of 4 variables
- Slides for ALH 2018
- Slides for TAMC 2019
Connecting Normalized Information Distance and Jaccard distance
I gave a talk in the online seminar “Computability Theory and Applications” on November 17, 2020, on
Normalized Information Distance and Jaccard distance.
The paper, with Niraula and Yoon, was published in Logical Foundations of Computer Science 2022.
Principles-based classification
I was the discussant for the following paper at Hawaii Accounting Research Conference 2020 on the UH Hilo campus:
The Contract Disclosure Mandate and Earnings Management under External Scrutiny
by Carlos Corona and Tae-Wook Ryan Kim
I learned that research in the Theory Track of the accounting discipline primarily is about mathematical modeling of the effects of government policies and business decisions. It borrows methods from economics for such modeling. In the case of the Corona-Kim paper: quadratic programming without constraints, and exponential utility functions. Usually these are not empirical papers, i.e., they don’t test the model explicitly against data. Indeed this would be hard to do with notions like “intensity of scrutiny”.
I am a discussant for “A theory of principles-based classification” by Konvalinka, Penno, and Stecher, at HARC 2021.
Jaccard distance and Normalized Information Distance
https://www.youtube.com/watch?v=t1rFAyPp7s0